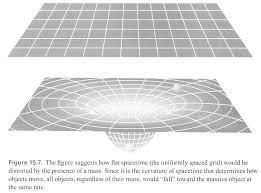
Représentation de la "courbure" de l'espace-temps.
Il résulte des études théoriques et de leurs applications que l'Univers est localement courbé par des champs de gravitation locaux autour des corps célestes, mais cette courbure n'est pas visible dans notre espace physique.
Ainsi, autour des plus simples des corps célestes, les astres sphériques (comme notre Soleil) la déformation existe. L'image souvent présentée, pour tenter de faire comprendre aux lecteurs ce qu'est cette "courbure" locale, est la suivante :
Une boule déformant par son poids une sorte de filet à mailles carrées.
Il s'agit en fait d'un trompe-l'oeil car rien de tout cela n'appartient à notre espace physique réel.
La théorie de la Relativité a mis en évidence la nécessité d'exprimer l'espace-temps dans un espace imaginaire à 4 dimensions ( les maths permettent cet artifice), le temps constituant la 4ème dimension (c.t) à ajouter aux 3 dimensions (x, y, z) de l'espace réel dans lequel nous vivons.
En effet, la métrique d'un espace plat en coordonnées cartésiennes ( celles qui ont été retenues pour la représentation du filet à mailles carrées ) s'exprime par l'élément infinitésimal : ds2 = c2dt2 - dx2 - dy2 - dz2 .
Ce trompe-l'oeil résulte de l'idée de représenter cet espace mathématique avec seulement 3 de ses 4 dimensions, ce qui est dès lors compatible avec notre vision.
L'espace-temps plat se déforme autour d'un corps massif à symétrie sphérique, en raison des forces de gravitation génèrées par ce dernier, mais il nous est impossible de visualiser directement cette déformation. Sous condition de ne conserver que 2 dimensions spatiales (plan horirontal) et la dimension du temps (sur la verticale), il est possible de faire un montage tridimensionnel artificiel.
Si l'on supprime la dimension spatiale z , ce ds2 se résume alors à ds2 = c2dt2 - dx2 - dy2 , la dimension c.dt occupant alors l'axe des z.
Remarque (1) : en supprimant la dimension spatiale z le corps sphérique attracteur devient un disque plan selon oxy (les auteurs des représentations conservent néanmoins le dessin d'une boule).
Remarque (2) : c'est une représentation mathématique qui est identique à elle-même quel que soit le plan oxy de l'espace réel passant par le centre du corps attractif ; elle n'est pas particulière à un plan diamétral, et elle n'est pas visible dans notre espace réel physique. Faire rouler une bille dans l'entonnoir ainsi formé est une pure illusion (mais qui a le mérite de plaire aux enfants).
De plus, s'agissant du champ de gravitation d'un corps à symétrie sphérique, l'espace autour est à symétrie sphérique : le choix d'un filet à mailles carrées n'est pas dutout approprié.
il y a beaucoup mieux à faire car le choix des coordonnées sphériques s'impose naturellement :
ds2 = c2dt2 - dr2 - r2d(téta)2 + r2sin2(téta).d(ksi)2 . Pour une distance radiale donnée r (sur une 2sphère), le ds2 = c2dt2 - dr2 - r2d(téta)2 .
Ainsi on obtient une représentation beaucoup plus judicieuse :
Exemple de la Terre avec l'orbite circulaire d'un satellite.
Ainsi la formule de Schwarzschild qui décrit la métrique autour d'un corps massif à symétrie sphérique s'écrit selon la direction radiale : ds2 = (1 + 2(phi)/c2).c2dt2 - (1 + 2(phi)/c2)-1.dr2 , avec (phi) : potentiel gravitationnel, lequel évolue selon le graphique figurant ci-après°.
Nota : °Hormis le cas de la singularité dite rayon de Schwarzschild r = RS = 2GM/c2 qui existe si RS > Rext (rayon extérieur de l'astre), ce qui correspond au cas du trou noir (lequel mérite une étude particulière en fonction de sa densité et sa compacité).
Il apparaît que le potentiel (phi) décroît continuement de 0 à l'infini, jusqu'à - 3/2 .G.M/R au centre, ce qui correspond toujours à une attraction jusqu'au centre du corps sphérique.
Avec cette formule cela donne, en considérant des observateurs immobiles , l'un local, sur la surface extérieure du corps sphérique (Φ = Φloc ), et l'autre à l'infini hors du champ de gravitation (Φ∞ = 0) : ds2 = Cte = (1 + 2Φloc/c2).c2dtloc 2 = c2 dt∞2 , soit dtloc = dt∞ /(1 + 2Φloc/c2)1/2
, soit dtloc > dt∞ car Φ < 0 : dilatation du temps.
Pour les champs gravitationnels faibles 2Φloc / c2 est faible vis à vis de 1, 1 /(1 + 2Φloc/c2)1/2 = 1 /(1 + Φloc/c2) = (1 - Φloc/c2) > 1 car - Φloc/c2 > 0 : la courbe représentative de ce coefficient a la même allure que la courbe du potentiel si l'axe des z est orienté vers le bas. Voilà bien l'explication de la représentation de la courbure de l'espace-temps :
Le creux correspond à l'axe des z orienté vers le bas.
En ce qui concerne la composante radiale de la métrique spatiale, faisons dt = 0, temps figé, et pour un observateur immobile dans le champ : , pour un observateur à l'infini Φloc = 0 → ds2 = Cte =
- (1 + 2Φloc/c2)-1.drloc2 = - dr∞2 , soit drloc = dr∞ (1 + 2Φloc/c2)1/2 : contraction de la composante radiale car Φ < 0 : les mailles du filet sont à resserrer près du corps attractif, aspect oublié par la plupart des représentations qui ne se préoccupent que de la courbure du temps et oublient la courbure de l'espace.
Mais en 1911 Einstein lui-même, s'il avait bien pris en compte l'effet de la dilatation du temps pour évaluer le ralentissement de la lumière, par contre il n'avait pas tenu compte de l'effet cumulé de la contraction de l'espace ... Il s'est rattrapé en 1916 !
_______________________